单源最短路径：Dijkstra 算法

计算机科学史伟大成就之一：Dijkstra 最短路径算法。这个算法适用于边的长度均不为负数的有向图，它计算从一个起始顶点到其它顶点的最短路径的长度。

单源最短路径问题

输入：有向图 $G=(V,E)$ ，起始顶点 $s\in V$ ，并且每条边 $e \in E$ 的长度 $l_e$ 均为非负值。

输出：每个顶点 $v\in V$ 的 $dist(s,v)$

注意： $dist(s,v)$ 这种记法表示从 $s$ 到 $v$ 的最短路径的长度（如果不存在从 $s$ 到 $v$ 的路径， $dist(s,v)$ 就是 $+\infty$ ）。

所谓路径的长度，就是组成这条路径的各条边的长度之和。

例如，如果一个图表示道路网，每条边的长度表示从一端到另一端的预期行车时间，那么单源最短路径问题就成为计算从一个起始顶点到 所有可能的目的地 的行车时间的问题。

边的长度可能为负的应用中，我们不应该使用 Dijkstra 算法，而应该使用比如 Bellman-Ford 算法。

Dijkstra 算法

Dijkstra 算法的整体结构和图的搜索算法相似。主循环每次迭代处理一个新的顶点。

算法的高级之处在于它采用了一种非常“聪明”的规则选择接下来处理哪个顶点：就是尚未处理的顶点中看上去 最靠近起始顶点 的那一个。

伪代码：

// 初始化
X := {s}
len(s) := 0, len(v) := +∞ 对于每个 v ≠ s
// 主循环
while 存在一条边(v, w), V ∈ X, w ∉ X, do
  (v*, w*) := 具有最小的 len(v) + lvw 的边
  把 w* 加入到 X 中
    len(w*) := len(v*) + lv*w*

集合 X 包含了这个算法已经处理过的顶点。一开始，X 只是包含了起始顶点 s（当然，len(s) =0）。这个集合 X 不断增长，直到它覆盖了从 s 到可以到达的所有顶点。

当这个算法把一个顶点添加到 X 时，它同时为这个顶点的 len 值赋一个有限的值。

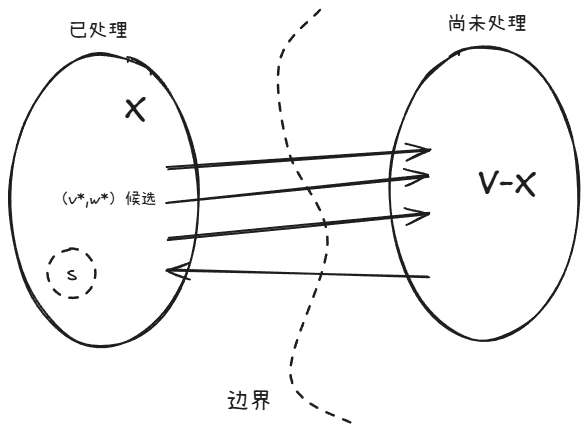
主循环的每次迭代向 X 添加一个新顶点，即某条从 X 跨越到 V-X 的边 (v, w) 的头顶点。（如果不存在这样的边，算法就会终止，对于所有的 v ∉ X，都有 len(v)=+∞）。

符合条件的如果有多条，选着最低的 (v*, w*)，它被定义为：

len(v) + l_{vw}

Dijkstra算法的每次迭代处理一个新顶点，即一条从X跨越到V−X的边的头顶点

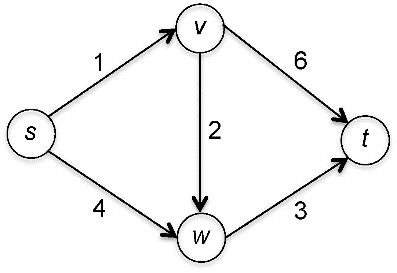
一个简单的实例

一个简单的图

一开始，集合 X 只包含了顶点 s，且 len(s)=0。
在主循环的第 1 次迭代中，有 (s,v) 和 (s,w) 两条边从 X 跨越到 V-X。得分分别是 $len(s)+l_{sv}=0+1=1$ 和 $len(s) + l_{sw}=0+4=4$ 。
- 由于前者分数更低，因此 v 加入到 X 的集合中，并且 len(v) 被赋予 (s,v) 的得分，就是 1。
第 2 次迭代中，X={s,v}，有 (s,w)、(v,w) 和 (v,t) 共 3 条边可以作为 (v*, w*) 的角色。得分是4、3 和 7。
- 由于 (v,w) 有最低的得分，因此 w 被添加到 X 中，len(w) 被赋值为 3。这时，X={s,v,w}。
第 3 次迭代中，(v, t) 和 (w, t) 的分数分别为 1+6=7 和 3+3=6，因此 len(t) 被设置为较小的值 6 。

现在，集合 X 包含了所有的顶点，不再有任何边从 X 跨越到 V-X 了，因此算法就宣告结束。

证明 Dijkstra 算法的正确性

定理（Dijkstra 算法的正确性）对于每个有向图 $G=(V,E)$ ，每个起始顶点 $s$ 并且所有边长均为 非负值，对于每个顶点 $v\in V$ ，Dijkstra 算法的结论 $len(v)=dist(s,v)$ 都成立。

归纳证法

我们的计划是根据主循环的迭代数量进行归纳，逐个计算 Dijkstra 算法的最短路径长度的正确性。

断言：定义 $P(k)$ 为在 Dijkstra 算法中，对于第 $k$ 个添加到 $X$ 中的顶点 $v$ ，存在 $len(v)=dist(s,v)$ .

通过数学归纳法进行证明的分为一个基础条件和一个归纳步骤两个部分。

基本条件：证明 $P(1)$ 是正确的。

我们知道第一个顶点 s 是起始顶点。因此 s 到它本身的最短路径是一条空路径，长度为 0。因此， $len(s)=0=dist(s,s)$ ，这就证明了 $P(1)$ 是成立的。

对于归纳步骤，我们选择 $k > 1$ 并假设 $P(1),\dots,P(k-1)$ 都是正确的。对于 Dijkstra 算法添加到 $X$ 的前 $k-1$ 个顶点， $len(v)=dist(s,v)$ 。

设 $w^*$ 表示添加到 $X$ 的第 $k$ 个顶点，并用 $(v^*，w^*)$ 表示在对应的那次迭代中所选的边。（此时 $v^*$ 必然已经在 $X$ 中）

算法把 $len(w^*)$ 赋值为这条边的得分，即 $len(v^*)+l_{v^*w^*}$ 。我们希望这个值和真正的最短路径长度 $dist(s,w^*)$ 相同。

我们分两个部分来证明这个结论的正确性。

Part 1

首先，我们证明真正的长度 $dist(s,w^*)$ 只可能小于算法所推测的 $len(w^*)$ ，即 $dist(s,w^*)\leqslant len(w^*)$ 。

由于当边 $(v^*,w^*)$ 被选中时， $v^*$ 已经在 $X$ 中，因此它是添加到 $X$ 的前 $k-1$ 个顶点之一。

根据归纳假设，Dijkstra 算法正确地计算了 $v^*$ 的最短路径长度： $len(v^*)=dist(s,v^*)$ .

具体来说，存在一条从 $s$ 到 $v^*$ 的路径 $P$ ，它的长度正好是 $len(v^*)$ 。

在 $P$ 的末端添加 $(v^*,w^*)$ 就产生了一条从 $s$ 到 $w^*$ 的路径 $P^*$ ，长度是 $len(v^*)+l_{v^*w^*}=len(w^*)$

$s-w^*$ 路径的最短路径除了候选路径 $P^*$ 之外不会再有其它路径，因此 $dist(s,w^*)$ 不可能大于 $len(w^*)$ 。

Part 2

现在，我们讨论反方向的不等式 $dist(s,w^*)\geqslant len(w^*)$ 。换言之，我们希望证明路径 $P^*$ 确实是 $s-w^*$ 的最短路径，与之竞争的 $s-w^*$ 路径的长度都不会小于 $len(w^*)$ 。

我们随意选一条 $s-w^*$ 的竞争路径 $P'$ ，我们不了解 $P'$ 。但是，我们知道它源自于 $s$ ，终于 $w^*$ 。迭代之初， $s$ 属于集合 $X$ ，但 $w^*$ 不属于 $X$ 。

由于它是从 $X$ 中开始并在 $X$ 之外结束，因此路径 $P'$ 跨越了 $X$ 和 $V-X$ 的边界 1 次。

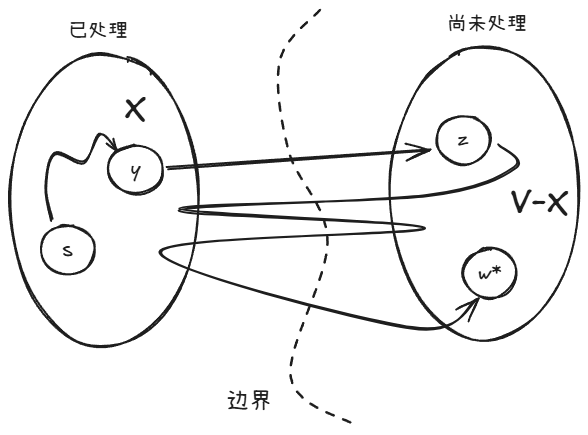
至少跨越 X 到 V-X 一次

设 $(y,z)$ 表示跨越边界的 $P'$ 的第 1 条边（ $y\in X$ 且 $z\notin X$ ）。

为了论证 $P'$ 的长度不会小于 $len(w^*)$ ，我们独立考虑它的三个部分：

$P'$ 从 $s$ 到 $y$ 的起始部分
边 $(y,z)$
从 $z$ 到 $w^*$ 的最终部分

起始部分不可能小于 $s$ 到 $y$ 的最短路径 $dist(s,y)$ ；边 $(y,z)$ 的长度是 $l_{yz}$ 。

最终部分我们并不是很清楚。但是，我们知道所有的边长度都是非负的。也就是说，它的总长度至少是 0。

将这三个部分的下界相加：

len(P')\geqslant dist(s,y)+l_{yz}+0

我们需要把下界和算法决策时的得分进行关联。

由于 $y\in X$ ，因此它是前 $k-1$ 个添加到 $X$ 的顶点之一。基于归纳假设，表明该算法会正确地计算它的最终路径长度： $dist(s,y)=len(y)$ 。

因此：

len(P')\geqslant len(y)+l_{yz}

右边正好是边 $(y,z)$ 的 Dijkstra 算法得分。由于总会选择最低的得分，并且因为在这次迭代中选了 $(v^*,w^*)$ 而不是 $(y,z)$ ，所以前者的 Dijkstra 得分更低：

len(v^*) + l_{v^*w^*}\leqslant len(y) + l_{yz}

因此：

len(P')\geqslant len(v^*) + l_{v^*w^*}=len(w^*)

这样就完成归纳步骤的第二部分，得出结论：

对于添加到集合 $X$ 的每个顶点 $v$ ，存在 $len(v)=dist(s,v)$ 。

最终验证

现在考虑一个从来没有被添加到 $X$ 的顶点 $v$ 。当这个算法结束时， $len(v)=+\infty$ 并且没有任何边从 $X$ 跨越到 $V-X$ 。

这意味着不存在从 $s$ 到 $v$ 的路径，因为这样的路径肯定会在某一处跨越边界。

因此， $dist(s,v)=+\infty$

我们可以得出结论，对于每个顶点 $v$ ，如果 $len(v)=dist(s,v)$ ，算法就会终止。不管 $v$ 是否被添加到 $X$ 。

至此，我们完成了整个证明过程。

一些新的研究

HHR+24

Universal Optimality of Dijkstra via Beyond-Worst-Case Heaps 这篇论文证明，Dijkstra 结合使用足够高效的数据结构时，在执行时间和比较次数方面具有普遍最优性（Universal Optimality）。

长久以来，Dijkstra 算法在最差情况下被认为是最佳的，例如使用 Fibonacci 堆时算法复杂度 $O(m+nlog(n))$ 。这篇论文进一步提升了对优势的理解，证明了在特定问题下（需要按距离排序输出结果），如果结合适当的数据结构。Dijkstra 实际上是普遍最优的。

DMMSY25

Breaking the Sorting Barrier for Directed Single-Source Shortest Paths 首次打破 Dijkstra 算法在稀疏图上的 $O(m+nlog(n))$ 时间限制。论文指出，如果不要求按距离排序输出结果，那么 Dijkstra 算法并不是最佳的。论文提出了 $O(m log_{\frac{2}{3}} n)$ 的算法。